고정 헤더 영역
상세 컨텐츠
본문
엔트로피의 정의 : 이산 확률 변수(연속적X), 불확실성을 계량화하기 위한 것. 예를들어, 주사위의 면이 각 1/6 일 때, 불확실성이 가장 높다.
정보를 압축하는데 한계가 있다.
수식을 보면,

이를 이용한, 예시를 두 개를 보겠다.

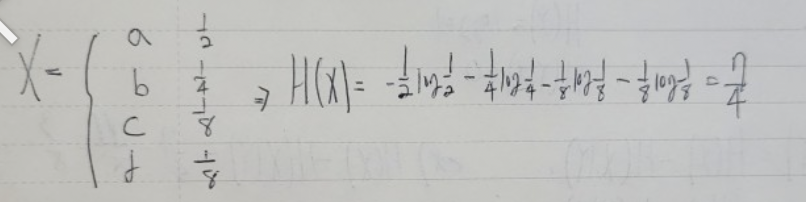
불확실성을 계량화 할 수도 있다. 엔트로피에 조건을 부여하면 된다.

이렇게만 보면 식이 어렵게 다가올 가능성이 높아, 예시를 통하여 다시 보겠다.

위 사진을 보고 식을 풀어보면,

조건을 어떻게 부여하고, 어디에 부여하느냐에 따라 값이 달라지는데, 이해의 편의를 위해 주사위를 예로 들겠다.

위에서 확인할 수 있듯이, 조건을 부여하지 않았을 때 값과, 부여했을 때 값이 다른 걸 확인할 수 있고, 어떤 변수에 조건을 부여하는지에
따라 값이 변하는 것을 확인할 수 있다.
이때 H(Y|X)=0인 이유는, X를 알면 Y의 불확실성이 사라졌다고 볼 수 있기 때문이다. X=2 이면 짝수인 것이 바로 정해지는 것 처럼.
mutual information(상호의존정보)는 두 확률에 대해 서로 얼마나 정보를 가지고 있는지 알 수 있다. 이것의 수식으로는

H(x) - H(X|Y)는 확률변수 Y가 확률변수 X의 정보를 얼마나 가지고 있는지에 따라 X의 불확실성이 줄어드는 것을 확인할 수 있다.
위에 식을 이용하여 계산하면,

최종적으로,
신경망의 손실함수에서 p를 라벨 k의 one-hot 벡터 t = (0,...,0,1,1,...,0)으로 잡고 q를 신경망이 예측한 확률벡터 (y0,y1,...,yn)으로
잡으면 H(p) = 0이므로
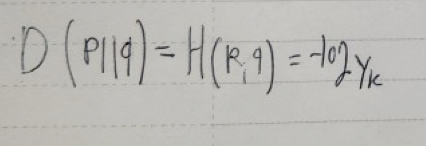
'연구실' 카테고리의 다른 글
| KeywordSpotting (1) | 2024.11.12 |
|---|---|
| KCC 한국 정보과학회 (0) | 2024.07.02 |
| 손실함수 (0) | 2024.01.27 |
| 신경망 구현 (0) | 2024.01.26 |
| MNIST (0) | 2024.01.25 |





